Conjoint Part-Worths Calculation
We use the following algorithm to calculate CBC Conjoint Part-Worths:
- NOTATION
Let there be R respondents, with individuals r = 1 ... R
Let each respondent see T tasks, with t = 1 ... T
Let each task t have C configurations (or concepts), with c = 1 ... C (C in our case is usually 3 or 4)
If we have A attributes, a = 1 to A, with each attribute having La levels, l = 1 to La, then the part-worth for a
particular attribute/level is w’(a,l). It is this (jagged array) of part worths we are solving for in this exercise. We can
simplify this to a one-dimensional array w(s), where the elements are:
{w’(1,1), w’(1,2) ... w’(1,L1), w’(2,1) ... w’(A,LA)} with w having S elements.A specific configuration x can be represented as a one-dimensional array x(s), where x(s)=1 if the specific
level/attribute is present, and 0 otherwise.
Let Xrtc represent the specific configuration of the cth configuration in the tth task for the rth respondent. Thus the
experiment design is represented by the four dimensional matrix X with size RxTxCxS
If respondent r chooses configuration c in task t then let Yrtc=1; otherwise 0.
- UTILITY OF A SPECIFIC CONFIGURATION
The Utility Ux of a specific configuration is the sum of the part-worths for those attribute/levels present in the configuration, i.e. it is the scalar product x.w
- THE MULTI-NOMIAL LOGIT MODEL
For a simple choice between two configurations, with utilities U1 and U2, the MNL model predicts that configuration 1 will be chosen
EXP(U1)/(EXP(U1) + EXP(U2)) of the time (a number between 0 and 1).
For a choice between N configurations, configuration 1 will be chosen
EXP(U1)/(EXP(U1) + EXP(U2) + ... + EXP(UN)) of the time.
- MODELED CHOICE PROBABILITY
Let the choice probability (using MNL model) of choosing the cth configuration in the tth task for the rth respondent be:
Prtc=EXP(xrtc.w)/SUM(EXP(xrt1.w), EXP(xrt2.w), ... , EXP(xrtC.w))
- LOG-LIKELIHOOD MEASURE
The Log-Likelihood measure LL is calculated as:
Prtc is a function of the part-worth vector w, which is the set of part-worths we are solving for.
- SOLVING FOR PART-WORTHS USING MAXIMUM LIKELIHOOD
We solve for the part-worth vector by finding the vector w that gives the maximum value for LL. Note that we are solving for S variables.
This is a multi-dimensional non-linear continuous maximization problem, and requires a standard solver library. We use the Nelder-Mead Simplex Algorithm.
The Log-Likelihood function should be implemented as a function LL(w, Y, X), and then optimized to find the vector w that gives us a maximum. The responses Y, and the design X are given, and constant for a specific optimization. Initial values for w can be set to the origin 0.
The final part-worths w are re-scaled so that the part-worths for any attribute have a mean of zero, simply by subtracting the mean of the part-worths for all levels of each attribute.
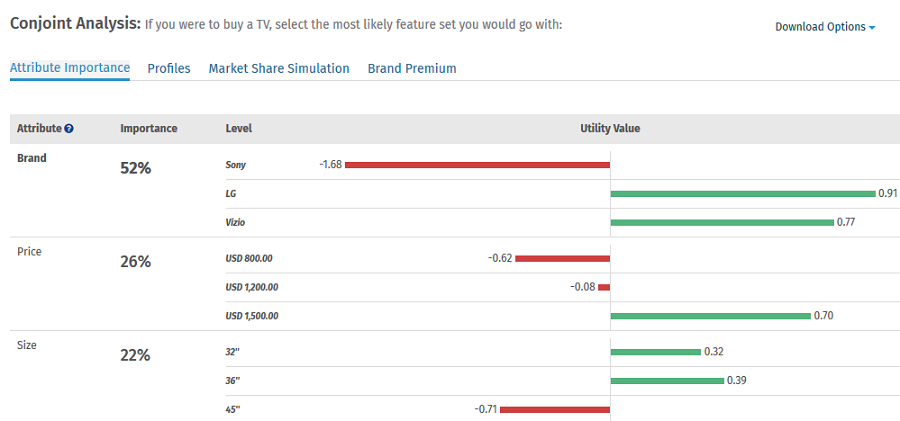
- Login » Surveys » Reports » Choice Modelling » Conjoint Analysis